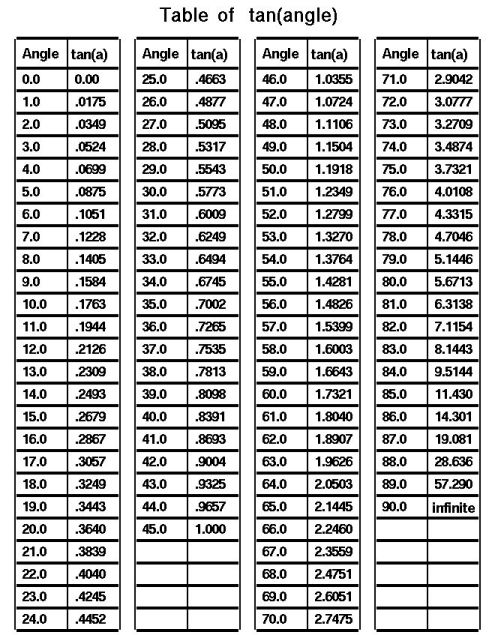
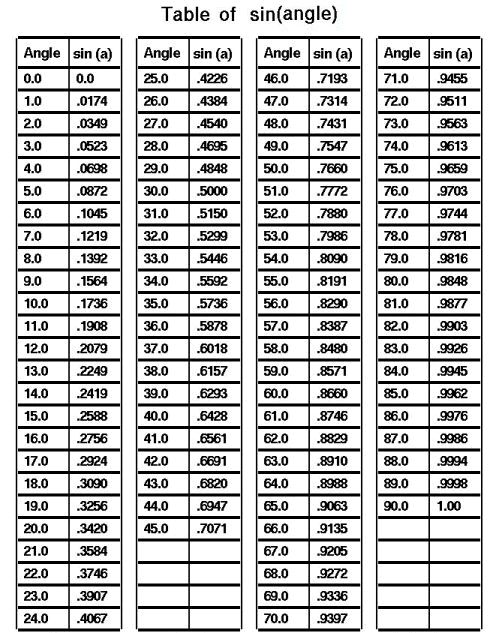
Trigonometry Tables

Below are the three basic trigonometry tables that when applied correctly by a knowledgeable user are extensively useful.

Pythagorean Theorem Below

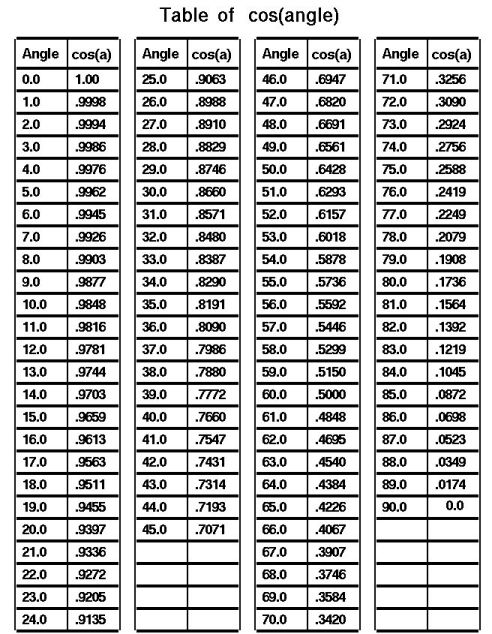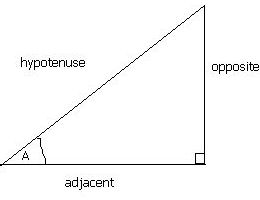
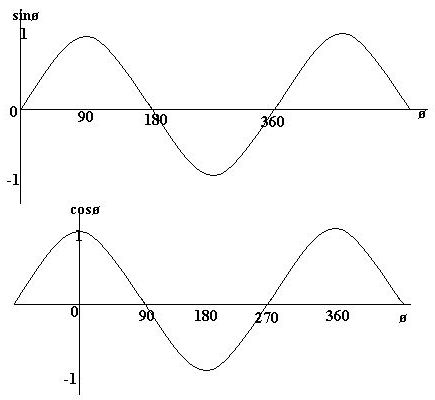
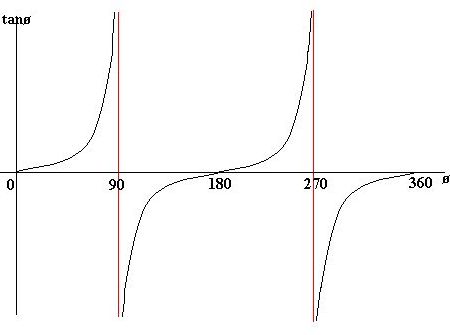
In any right angled triangle, for any angle:

the length of the opposite side = The sin of the angle
the length of the hypotenuse

the length of the adjacent side = The cos of the angle
the length of the hypotenuse

the length of the opposite side = The tan of the angle
the length of the adjacent side

The hypotenuse of a right angled triangle is the longest side, which is the one opposite the right angle. The adjacent side is the side which is between the angle in question and the right angle. The opposite side is opposite the angle in question.

sin = o/h cos = a/h tan = o/a
Often remembered by: soh cah toa

Graphing sin, cos and tan

Notes:

The graphs of sin and cos are have a repeating period of 360°. The graphs repeat themselves every 360°. The graph of cos is the same as the graph of sin shifted 90° to the right/ left. For this reason, sin(x) = cos(90 - x) and cos(x) = sin(90 - x). Cos is an even function. It is symmetrical in the y-axis. Sin is an odd function.

The graph of tan has asymptotes (line which gets very close to, but does not touch). The red lines are asymptotes.

These graphs obey the usual laws of graph transformations.

Pythagorean Theorem

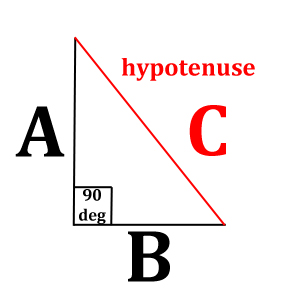In any right-angled (one angle is exactly 90 degrees) triangle, the square of the length of the hypotenuse (C - the side opposite the right angle) is equal to the sum of the squares of the other two (A, B) sides. The Pythagorean theorem can be expressed as the Pythagorean equation:
A² + B² = C²
C=square root of ( A² + B² )
A=square root of ( C² - B² )
B=square root of ( C² - A² )

Finding square roots of numbers without a calculator
1. Estimate - first, get as close as you can by finding two perfect square roots your number is between.
2. Divide - divide your number by the smaller estimated number.
3. Average - take the average of the result of step 2 and the root.
4. Use the result of step 3 or repeat steps 2 and 3 until you have a number that is accurate enough for you.

Example:
Calculate the square root of 10 to 2 decimal places.

Solution:
1. 3 squared = 9 and 4 squared = 16, therefore the square root of 10 is between 3 and 4.
2. Divide 10 by 3 [10/3 = 3.33 (you can round off your answer)]
3. Average 3.33 and 3 [(3.33 + 3)/2 = 3.1667]
4. Repeat step 2 [10/3.1667 = 3.1579]
5. Repeat step 3: Average 3.1579 and 3.1667 [(3.1579 + 3.1667)/2 = 3.1623]
6. Try the answer - Is 3.1623 squared equal to 10? [3.1623 x 3.1623 = 10.0001]
7. If this is accurate enough for you, you can stop! Otherwise, you can repeat steps 2 and 3.

↑ Recommend ZRD